-
 Home
Home
-
 News
News
Latest Educational News Stories
Daily update of all national, international news, picture stories, college / university announcements and educational events.
-
 Colleges
Colleges
Pakistan's Largest Database of Colleges and Universities
Explore Largest Directory of Private and Govt. Colleges, Universities and find best institute for your future Education.
-
 Courses
Courses
-
 Admission
Admission
-
 Lectures
Lectures
-
 Online Test
Online Test
Short Question
- 9th Class Physics Short Questions
- 9th Class Chemistry Short Questions
- 9th Class Math Short Questions
- 9th Class Biology Short Questions
- 9th Class Computer Short Questions
- 9th Class English Short Questions
- 10th Class Physics Short Question
- 10th Class Chemistry Short Question
- 10th Class Math Short Question
- 10th Class Biology Short Question
- 10th Class Computer Short Question
- 10th Class English Short Question
-
 Past Papers
Past Papers
-
 Date Sheets
Date Sheets
-
 Results
Results
Exam Results 2024
Check online Results 2024 Matric Inter BA BSc B.Com MA MSc M.Com CSS PCS MCAT ECAT of all educational boards and universities in Pakistan
-
 Study Abroad
Study Abroad
Study Abroad Programs and Opportunities for Pakistani Students
Explore free study abroad search to find programs, consultants, events to study in USA, UK, Australia, China, Malaysia and many others.
-
 Jobs
Jobs
-
 Tutors
Tutors
-
 More
More
-
 Apps
Apps
This online test contains MCQs about following topics:
Introduction - Principle of Mathematical Induction - Principle of Extended Mathematical Induction - Binomial Theorem - The Binomial Theorem when the index n is a negative Integer or a FRACTION - Application of the Binomial Theorem
FA Part 1 Mathematics Ch. 8 Test

FA Part 1 English Medium Subjects
FA Part 1 Urdu Medium Subjects
11th Class FA Mathematics Chapter 8 Online Test
Try The 11th Class FA Mathematics Chapter 8 Online Test
-
Total Questions20
-
Time Allowed30
Question # 1
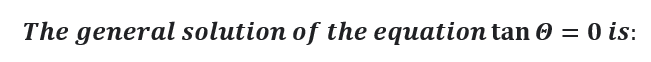
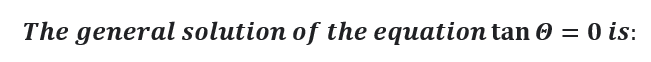
Question # 2


Question # 3
if sin x + cos x = 0, then x = _________:
Question # 4


Question # 5


Question # 6


Question # 7
The solution set of 2cosΘ + √3 = 0 is:
Question # 8
Trigonometric equation has _________ solutions:
Question # 9
Which trigonometric equation has secondary solution ?
Question # 10
The general solution of sin x = cos x is ___________:
Question # 11


Question # 12


Question # 13
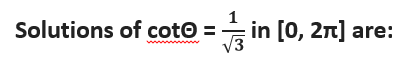
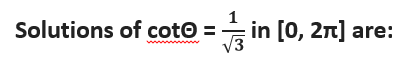
Question # 14


Question # 15
The solution set of sinΘ, cosΘ = 1 in [0, 2π] is ___________:
Question # 16


Question # 17
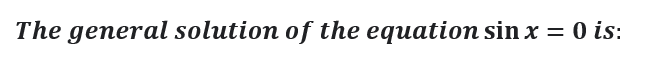
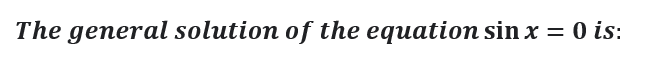
Question # 18


Question # 19
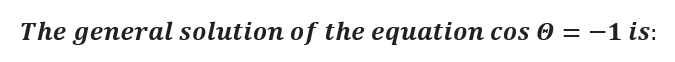
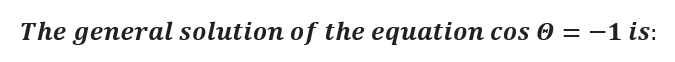
Question # 20
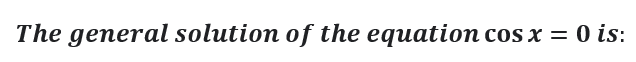
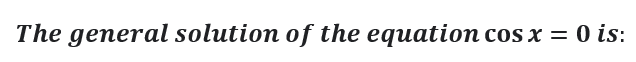
Here is List Of Chapter Wise Tests
| Ch. # | Test Name | MCQs Available | PDF File | Launch Test |
|---|---|---|---|---|
| 1 | 11th Class FA Mathematics Chapter 1 Test Online | 0 | Download PDF | Launch Test |
| 2 | 11th Class FA Mathematics Chapter 2 Online Test | 0 | Download PDF | Launch Test |
| 3 | 11th Class FA Mathematics Chapter 3 Online Test | 0 | Download PDF | Launch Test |
| 4 | 11th Class FA Mathematics Chapter 4 Online Test | 0 | Download PDF | Launch Test |
| 5 | 11th Class FA Mathematics Chapter 5 Online Test | 0 | Download PDF | Launch Test |
| 6 | 11th Class FA Mathematics Chapter 6 Online Test | 0 | Download PDF | Launch Test |
| 9 | 11th Class FA Mathematics Chapter 9 Online Test | 0 | Download PDF | Launch Test |
| 10 | 11th Class FA Mathematics Chapter 10 Online Test | 0 | Download PDF | Launch Test |
| 11 | 11th Class FA Mathematics Chapter 11 Online Test | 0 | Download PDF | Launch Test |
| 12 | 11th Class FA Mathematics Chapter 12 Online Test | 0 | Download PDF | Launch Test |
| 13 | 11th Class FA Mathematics Chapter 13 Online Test | 0 | Download PDF | Launch Test |
Top Scorers of 11th Class FA Mathematics Chapter 8 Online Test
-
A Ahmaf 05 - Jul - 2021 06 Min 41 Sec 19/20 -
R Romee 08 - May - 2019 07 Min 15 Sec 19/20 -
M Marwa Ashfaq 14 - May - 2024 13 Min 07 Sec 15/20 -
H Hamza mirani 16 - May - 2024 14 Min 11 Sec 15/20 -
A Ar Rehman 14 - Jul - 2024 15 Min 27 Sec 14/20 -
M Mubashar 15 - Jul - 2022 01 Min 16 Sec 13/20 -
A asad ijaz 14 - Jun - 2023 02 Min 44 Sec 13/20 -
D Dileep Moolani 02 - Jul - 2023 01 Min 34 Sec 12/20 -
S Syed Saad Ali 07 - Dec - 2023 04 Min 16 Sec 12/20 -
M Mishal Arshad 07 - Sep - 2024 11 Min 41 Sec 12/20 -
H Hamza 27 - Jul - 2021 51 Min 04 Sec 12/20 -
Y Yar Muhammad Khuwaja 20 - Nov - 2023 01 Min 00 Sec 11/20 -
S Shehzad Ahmad 25 - Nov - 2023 01 Min 28 Sec 11/20 -
T Talha 20 - Nov - 2021 04 Min 50 Sec 11/20 -
F Fatima 05 - Jun - 2021 10 Min 58 Sec 11/20
FSc Part 1 Mathematics (New Book) Important MCQ's
| Sr.# | Question | Answer |
|---|---|---|
| 1 | The general solution of sin x = cos x is ___________: |
A. nπ
B. 2nπ
|
| 2 |

|
|
| 3 | if sin x + cos x = 0, then x = _________: |
D. none of these
|
| 4 |

|
|
| 5 |

|
|
| 6 |

|
|
| 7 |

|
|
| 8 |

|
|
| 9 | The solution set of sinΘ, cosΘ = 1 in [0, 2π] is ___________: |
A. 0
C. solution does not exist
|
| 10 |

|
FA Part 1 Mathematics Chapter 8 Test
Here you can prepare FA Part 1 Mathematics Chapter 8 Mathematical Induction and Binomial Theorem Test. Click the button for 100% free full practice test.








.jpg)
























Share your comments & questions here
No comments yet. Be the first to comment!